8. Preblur for fermionic functions

Demo script for preblur for fermionic functions. Note that the example is somewhat extreme.

import numpy as np
import matplotlib.pyplot as plt
import sys, os
sys.path.insert(0, os.environ['HOME']+'/Programs/ana_cont')
import ana_cont.continuation as cont

wgrid_full = np.linspace(-10., 10., num=2001, endpoint=True)
spectrum_true = np.exp(-(wgrid_full-0.5)**2/(2.*1.**2))
spectrum_true /= np.trapz(spectrum_true, wgrid_full)
beta = 20.
niw = 50
noise_ampl = 0.005
rng = np.random.RandomState(321)
noise = noise_ampl * (rng.randn((niw)) + 1j * rng.randn((niw))) / np.sqrt(2)
wn = np.pi/beta * (2.*np.arange(niw) + 1.)
giw_pure = np.trapz(spectrum_true[None,:]/(1j*wn[:,None] - wgrid_full[None,:]), wgrid_full, axis=1)
giw = giw_pure + noise
fig,ax = plt.subplots(ncols=2, nrows=1, figsize=(15,7))
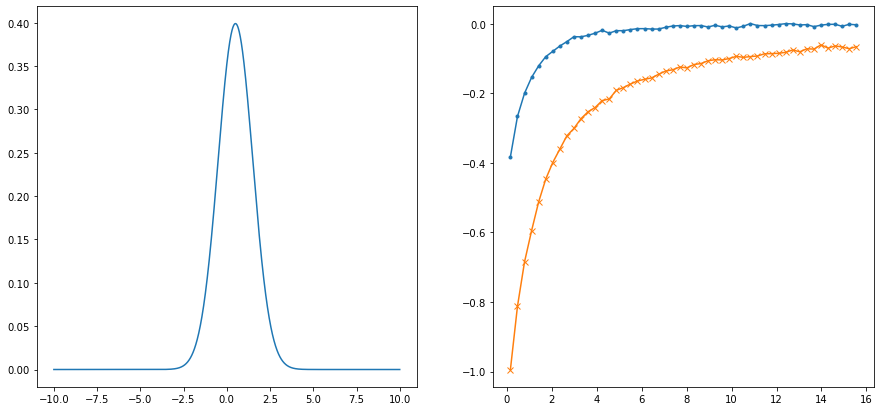
ax[0].plot(wgrid_full, spectrum_true)
ax[1].plot(wn, giw.real, marker='.')
ax[1].plot(wn, giw.imag, marker='x')
plt.show()

nw = 301
w = 10. * np.tan(np.linspace(-np.pi/2.1, np.pi/2.1, num=nw, endpoint=True)) / np.tan(np.pi/2.1)
# w = np.linspace(-10., 10., num=nw, endpoint=True)
# model = np.ones_like(w)
model = np.exp(-(w/8.)**6)
model /= np.trapz(model, w)
probl = cont.AnalyticContinuationProblem(im_axis=wn, re_axis=w, im_data=giw, kernel_mode='freq_fermionic')
sol,_ = probl.solve(method='maxent_svd', stdev=np.ones_like(wn)*noise_ampl,
                    alpha_determination='chi2kink', optimizer='newton', model=model)
fig,ax = plt.subplots(ncols=2, nrows=1, figsize=(15,7))
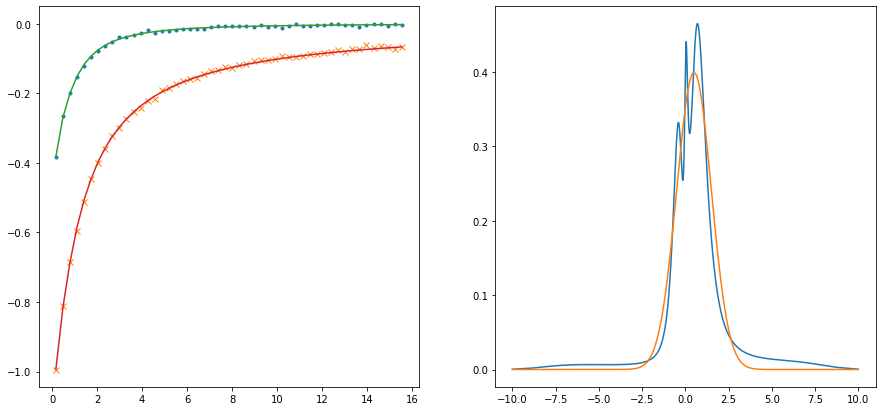
ax[0].plot(wn, giw.real, marker='.', linestyle='None')
ax[0].plot(wn, giw.imag, marker='x', linestyle='None')
ax[0].plot(wn, sol.backtransform.real)
ax[0].plot(wn, sol.backtransform.imag)
ax[1].plot(w, sol.A_opt)
ax[1].plot(wgrid_full, spectrum_true)
plt.show()

301 data points on real axis
100 data points on imaginary axis
36 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00,    chi2 = 8.389e+04,   S = -2.096e-09,   nfev = 5,   norm = 1.000
log10(alpha) = 8.00,    chi2 = 8.381e+04,   S = -2.097e-07,   nfev = 11,   norm = 1.000
log10(alpha) = 7.00,    chi2 = 8.306e+04,   S = -2.103e-05,   nfev = 15,   norm = 1.003
log10(alpha) = 6.00,    chi2 = 7.538e+04,   S = -2.139e-03,   nfev = 18,   norm = 1.033
log10(alpha) = 5.00,    chi2 = 2.488e+04,   S = -1.177e-01,   nfev = 20,   norm = 1.239
log10(alpha) = 4.00,    chi2 = 2.576e+03,   S = -3.889e-01,   nfev = 26,   norm = 1.354
log10(alpha) = 3.00,    chi2 = 3.076e+02,   S = -6.918e-01,   nfev = 30,   norm = 1.172
log10(alpha) = 2.00,    chi2 = 5.230e+01,   S = -1.013e+00,   nfev = 20,   norm = 1.051
log10(alpha) = 1.00,    chi2 = 3.738e+01,   S = -1.167e+00,   nfev = 20,   norm = 1.016
log10(alpha) = 0.00,    chi2 = 3.675e+01,   S = -1.264e+00,   nfev = 36,   norm = 1.010
log10(alpha) = -1.00,   chi2 = 3.644e+01,   S = -1.832e+00,   nfev = 58,   norm = 1.010
log10(alpha) = -2.00,   chi2 = 3.634e+01,   S = -3.048e+00,   nfev = 31,   norm = 1.011
log10(alpha) = -3.00,   chi2 = 3.633e+01,   S = -4.155e+00,   nfev = 31,   norm = 1.011
Optimal log alpha 1.9959041814096288
log10(alpha) = 2.00,    chi2 = 5.208e+01,   S = -1.014e+00,   nfev = 8,   norm = 1.051

probl = cont.AnalyticContinuationProblem(im_axis=wn, re_axis=w, im_data=giw, kernel_mode='freq_fermionic')
sol,_ = probl.solve(method='maxent_svd',
                    stdev=np.ones_like(wn)*noise_ampl*1.,
                    alpha_determination='chi2kink',
                    optimizer='newton',
                    model=model,
                    preblur=True,
                    blur_width=0.45)
fig,ax = plt.subplots(ncols=2, nrows=1, figsize=(15,7))
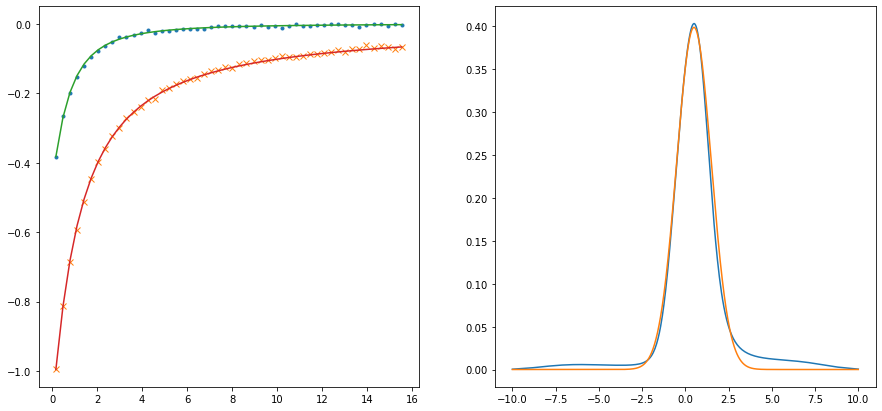
ax[0].plot(wn, giw.real, marker='.', linestyle='None')
ax[0].plot(wn, giw.imag, marker='x', linestyle='None')
ax[0].plot(wn, sol.backtransform.real)
ax[0].plot(wn, sol.backtransform.imag)
ax[1].plot(w, sol.A_opt)
ax[1].plot(wgrid_full, spectrum_true)
plt.show()

301 data points on real axis
100 data points on imaginary axis
32 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00,    chi2 = 8.393e+04,   S = -1.616e-09,   nfev = 5,   norm = 1.000
log10(alpha) = 8.00,    chi2 = 8.387e+04,   S = -1.616e-07,   nfev = 11,   norm = 1.000
log10(alpha) = 7.00,    chi2 = 8.329e+04,   S = -1.616e-05,   nfev = 14,   norm = 1.003
log10(alpha) = 6.00,    chi2 = 7.750e+04,   S = -1.606e-03,   nfev = 18,   norm = 1.033
log10(alpha) = 5.00,    chi2 = 3.488e+04,   S = -1.061e-01,   nfev = 21,   norm = 1.256
log10(alpha) = 4.00,    chi2 = 2.658e+03,   S = -5.150e-01,   nfev = 35,   norm = 1.365
log10(alpha) = 3.00,    chi2 = 3.171e+02,   S = -8.097e-01,   nfev = 22,   norm = 1.168
log10(alpha) = 2.00,    chi2 = 5.553e+01,   S = -1.132e+00,   nfev = 22,   norm = 1.047
log10(alpha) = 1.00,    chi2 = 4.054e+01,   S = -1.305e+00,   nfev = 21,   norm = 1.011
log10(alpha) = 0.00,    chi2 = 3.894e+01,   S = -1.562e+00,   nfev = 37,   norm = 1.007
log10(alpha) = -1.00,   chi2 = 3.837e+01,   S = -2.437e+00,   nfev = 73,   norm = 1.009
log10(alpha) = -2.00,   chi2 = 3.828e+01,   S = -3.584e+00,   nfev = 46,   norm = 1.009
log10(alpha) = -3.00,   chi2 = 3.827e+01,   S = -4.686e+00,   nfev = 32,   norm = 1.009
Optimal log alpha 2.0794519212086
log10(alpha) = 2.08,    chi2 = 5.996e+01,   S = -1.112e+00,   nfev = 13,   norm = 1.052