[1]:
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.insert(0, '../..')
import ana_cont.continuation as cont
4. Square lattice Hubbard model, \(U=2\), \(\beta=5\), half-filling¶
4.1. Analytic continuation of self-energy¶
[2]:
# load data
siw = np.load('data/square_U2_b5/siw.npy')
err = np.load('data/square_U2_b5/siw_err.npy')
beta = 5.
mu = 1.
[3]:
# define the problem
niw = 100 # number of Matsubara frequencies
wn = np.pi / beta * (2. * np.arange(niw) + 1.) # fermionic Matsubara frequencies
w = np.linspace(-20., 20., num=501, endpoint=True) # real-frequency grid
model = np.ones_like(w) # flat default model
model /= np.trapz(model, w) # normalization, not strictly necessary
# the problem is defined by: imaginary grid, real grid, data, kernel type
probl = cont.AnalyticContinuationProblem(im_axis=wn, # imaginary grid
re_axis=w, # real grid
im_data=1j * siw.imag[:niw], # data
kernel_mode='freq_fermionic') # kernel type
[4]:
# most basic way to solve the problem
sol, _ = probl.solve(method='maxent_svd', # Maxent solver that works with singular value decomp.
optimizer='newton', # newton root finding for the optimization problem
alpha_determination='chi2kink',
model=model, # default model
stdev=err[:niw], # standard deviation of the data
alpha_start=1e12, # largest alpha, starting value
interactive=True)
501 data points on real axis
200 data points on imaginary axis
31 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 12.00, chi2 = 4.238e+06, S = -5.061e-11, nfev = 2, norm = 1.000
log10(alpha) = 11.00, chi2 = 4.236e+06, S = -5.058e-09, nfev = 8, norm = 1.000
log10(alpha) = 10.00, chi2 = 4.218e+06, S = -5.030e-07, nfev = 11, norm = 1.001
log10(alpha) = 9.00, chi2 = 4.045e+06, S = -4.756e-05, nfev = 14, norm = 1.008
log10(alpha) = 8.00, chi2 = 2.898e+06, S = -2.878e-03, nfev = 17, norm = 1.062
log10(alpha) = 7.00, chi2 = 1.088e+06, S = -3.482e-02, nfev = 18, norm = 1.179
log10(alpha) = 6.00, chi2 = 2.258e+05, S = -1.751e-01, nfev = 22, norm = 1.133
log10(alpha) = 5.00, chi2 = 2.230e+04, S = -4.523e-01, nfev = 55, norm = 1.047
log10(alpha) = 4.00, chi2 = 1.078e+03, S = -6.940e-01, nfev = 26, norm = 1.012
log10(alpha) = 3.00, chi2 = 8.521e+01, S = -8.045e-01, nfev = 32, norm = 1.003
log10(alpha) = 2.00, chi2 = 4.769e+01, S = -8.460e-01, nfev = 23, norm = 1.001
log10(alpha) = 1.00, chi2 = 4.528e+01, S = -8.820e-01, nfev = 36, norm = 1.001
log10(alpha) = 0.00, chi2 = 4.411e+01, S = -1.084e+00, nfev = 43, norm = 1.000
log10(alpha) = -1.00, chi2 = 4.371e+01, S = -1.722e+00, nfev = 48, norm = 1.000
log10(alpha) = -2.00, chi2 = 4.362e+01, S = -2.824e+00, nfev = 31, norm = 1.000
log10(alpha) = -3.00, chi2 = 4.362e+01, S = -3.880e+00, nfev = 39, norm = 1.000
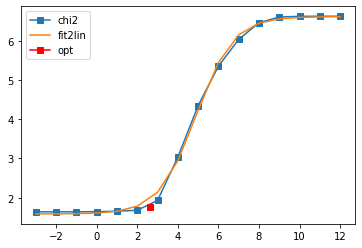
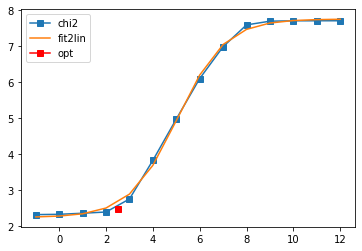
Fit parameters [1.58559603 5.0305896 4.91072294 1.09647514]
Optimal log alpha 2.6306894961847327
log10(alpha) = 2.63, chi2 = 5.803e+01, S = -8.241e-01, nfev = 17, norm = 1.002
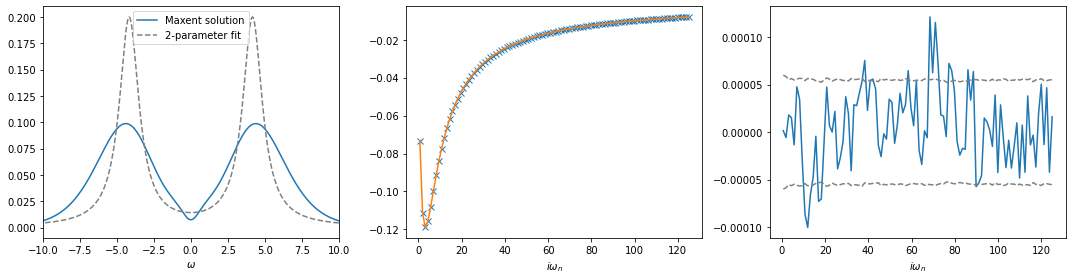
[5]:
# load fitted self-energy
w_fit, sw_fit = np.load('data/square_U2_b5/sw_fit.npy').T
#plot results
fig, ax = plt.subplots(ncols=3, nrows=1, figsize=(15, 4))
ax[0].plot(w, sol.A_opt, label='Maxent solution')
ax[0].plot(w_fit, sw_fit, color='gray', ls='--', label='2-parameter fit')
ax[0].legend()
ax[0].set_xlim(-10., 10.)
ax[0].set_xlabel(r'$\omega$')
ax[1].plot(wn, siw.imag[:niw], marker='x', ls='None')
ax[1].plot(wn, sol.backtransform.imag)
ax[1].set_xlabel(r'$i\omega_n$')
ax[2].plot(wn, (siw[:niw] - sol.backtransform).imag)
ax[2].plot(wn, err[:niw], ls='--', color='gray')
ax[2].plot(wn, -err[:niw], ls='--', color='gray')
ax[2].set_xlabel(r'$i\omega_n$')
plt.tight_layout()
plt.show()
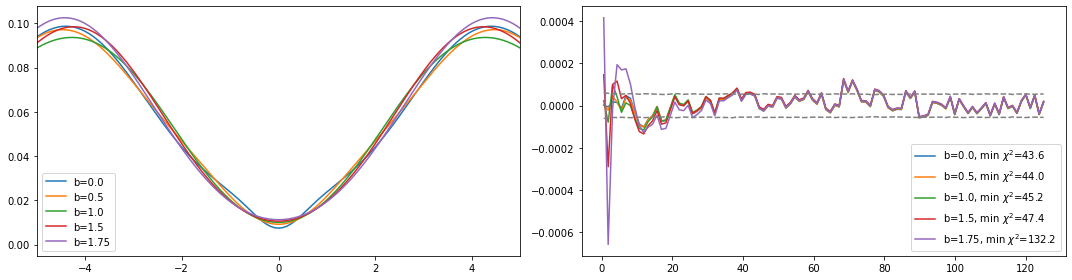
[6]:
# more sophisticated solution, using preblur
bw = [0., 0.5, 1., 1.5, 1.75] # some values for the blur width
bt_list = [] # here we store the backtransform arrays
spec_list = [] # here we store the spectral functions
chi_list= [] # here we store the chi2 deviation
for i in range(len(bw)): # loop over some values of the blur width
sol, sol_all = probl.solve(method='maxent_svd', # Maxent solver that works with singular value decomp.
optimizer='newton', # newton root finding for the optimization problem
alpha_determination='chi2kink',
model=model, # default model
stdev=err[:niw], # standard deviation of the data
preblur=bw[i]>0., # switch on preblur if blur_width > 0.
blur_width=bw[i], # 1. is good, 1.5 is limit
alpha_start=1e12, # largest alpha, starting value
interactive=False,
verbose=False)
bt_list.append(sol.backtransform)
spec_list.append(sol.A_opt)
chi_list.append(sol_all[-1].chi2)
[7]:
#plot results
fig, ax = plt.subplots(ncols=2, nrows=1, figsize=(15, 4))
for i in range(len(bw)):
ax[0].plot(w, spec_list[i], label='b={}'.format(bw[i]))
ax[0].legend()
ax[0].set_xlim(-5., 5.)
for i in range(len(bw)):
ax[1].plot(wn, (siw[:niw] - bt_list[i]).imag,
label='b={}, min $\chi^2$={:.1f}'.format(bw[i], chi_list[i]))
ax[1].plot(wn, err[:niw], ls='--', color='gray')
ax[1].plot(wn, -err[:niw], ls='--', color='gray')
ax[1].legend()
plt.tight_layout()
plt.show()
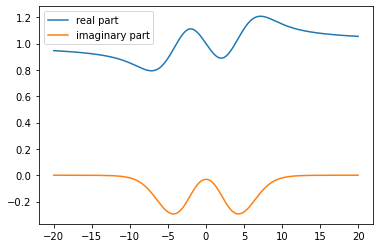
[8]:
# take b=1., which is list element #2 (in zero-based indexing)
sw = cont.GreensFunction(spectrum=spec_list[2], wgrid=w, kind='fermionic').kkt() + 1.
[9]:
plt.plot(w, sw.real, label='real part')
plt.plot(w, sw.imag, label='imaginary part')
plt.legend()
plt.show()
4.2. Calculate spectrum from self-energy and DOS¶
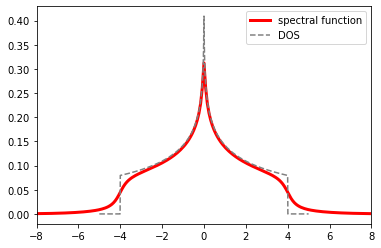
In cases where the self-energy is proportional to a unit matrix in orbital space, we can calculate the spectral function from the non-interacting DOS \(A_0(\omega)\) and the self-energy in real frequencies as
[10]:
from scipy.special import ellipk
w_dos = np.linspace(-5., 5., num=1000, endpoint=True)
dos = np.nan_to_num(ellipk(np.sqrt(1. - (w_dos / 4.)**2)**2) / (2. * np.pi**2))
<ipython-input-10-eed5e07aad46>:3: RuntimeWarning: invalid value encountered in sqrt
dos = np.nan_to_num(ellipk(np.sqrt(1. - (w_dos / 4.)**2)**2) / (2. * np.pi**2))
[11]:
g_from_s = np.trapz(dos[None, :]
/ (w[:, None] + mu - w_dos[None, :] - sw[:, None]),
w_dos, axis=1)
[12]:
plt.plot(w, -g_from_s.imag / np.pi, color='red', lw=3., label='spectral function')
plt.plot(w_dos, dos, color='gray', ls='--', label='DOS')
plt.xlim(-8., 8.)
plt.legend()
plt.show()
4.3. Direct analytic continuation of the Green’s function¶
[13]:
giw = np.load('data/square_U2_b5/giw.npy')
err_g = np.ones_like(giw, dtype=np.float) * 1e-4
[14]:
niw_g = 100
iw_g = np.pi / beta * (2. * np.arange(niw_g) + 1.)
w_g = np.linspace(-12., 12., num=501, endpoint=True)
model = np.ones_like(w_g)
model /= np.trapz(model, w_g) # normalization, not strictly necessary
probl = cont.AnalyticContinuationProblem(im_axis=iw_g,
re_axis=w_g,
im_data=1j * giw.imag[:niw_g],
kernel_mode='freq_fermionic')
[15]:
sol, _ = probl.solve(method='maxent_svd',
optimizer='newton',
alpha_determination='chi2kink',
model=model,
stdev=err_g[:niw_g],
interactive=True,
alpha_start=1e11,
alpha_end=1e-4)
501 data points on real axis
200 data points on imaginary axis
27 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 11.00, chi2 = 2.113e+07, S = -1.867e-08, nfev = 6, norm = 1.000
log10(alpha) = 10.00, chi2 = 2.106e+07, S = -1.866e-06, nfev = 12, norm = 1.001
log10(alpha) = 9.00, chi2 = 2.039e+07, S = -1.857e-04, nfev = 15, norm = 1.011
log10(alpha) = 8.00, chi2 = 1.432e+07, S = -1.636e-02, nfev = 18, norm = 1.102
log10(alpha) = 7.00, chi2 = 1.698e+06, S = -2.150e-01, nfev = 18, norm = 1.281
log10(alpha) = 6.00, chi2 = 2.101e+05, S = -4.029e-01, nfev = 21, norm = 1.173
log10(alpha) = 5.00, chi2 = 1.556e+04, S = -6.481e-01, nfev = 22, norm = 1.056
log10(alpha) = 4.00, chi2 = 9.667e+02, S = -8.289e-01, nfev = 38, norm = 1.013
log10(alpha) = 3.00, chi2 = 2.968e+01, S = -9.280e-01, nfev = 35, norm = 1.003
log10(alpha) = 2.00, chi2 = 1.042e+00, S = -9.596e-01, nfev = 20, norm = 1.000
log10(alpha) = 1.00, chi2 = 1.699e-02, S = -9.698e-01, nfev = 27, norm = 1.000
log10(alpha) = 0.00, chi2 = 7.127e-04, S = -9.713e-01, nfev = 21, norm = 1.000
log10(alpha) = -1.00, chi2 = 2.308e-04, S = -9.720e-01, nfev = 19, norm = 1.000
log10(alpha) = -2.00, chi2 = 1.796e-04, S = -9.726e-01, nfev = 31, norm = 1.000
log10(alpha) = -3.00, chi2 = 1.649e-04, S = -9.754e-01, nfev = 39, norm = 1.000
log10(alpha) = -4.00, chi2 = 1.446e-04, S = -1.019e+00, nfev = 29, norm = 1.000
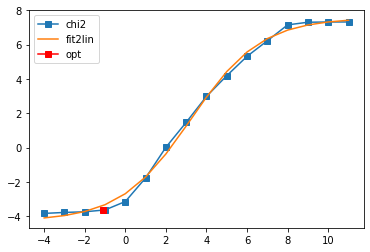
Fit parameters [-4.28238488 11.83879519 3.22272695 0.5777884 ]
Optimal log alpha -1.1041165907794408
log10(alpha) = -1.10, chi2 = 2.173e-04, S = -9.721e-01, nfev = 11, norm = 1.000
[16]:
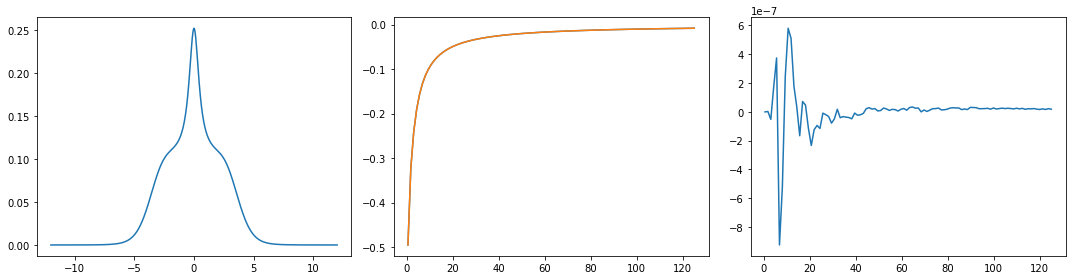
fig, ax = plt.subplots(ncols=3, nrows=1, figsize=(15, 4))
ax[0].plot(w_g, sol.A_opt)
ax[1].plot(iw_g, giw.imag[:niw_g])
ax[1].plot(iw_g, sol.backtransform.imag)
ax[2].plot(iw_g, (giw[:niw_g] - sol.backtransform).imag)
plt.tight_layout()
plt.show()
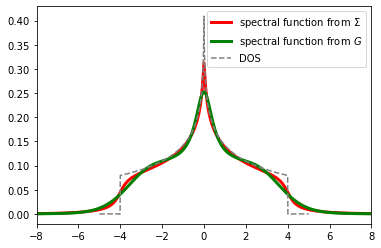
[17]:
plt.plot(w, -g_from_s.imag / np.pi, color='red', lw=3., label=r'spectral function from $\Sigma$')
plt.plot(w_g, sol.A_opt, color='green', alpha=1., lw=3., label=r'spectral function from $G$')
plt.plot(w_dos, dos, color='gray', ls='--', label='DOS')
plt.xlim(-8., 8.)
plt.legend()
plt.show()
5. Strontium vanadate¶
[18]:
siw = np.load('data/svo/siw.npy')
err = np.load('data/svo/siw_err.npy')
hartree = np.load('data/svo/hartree.npy')
beta = np.load('data/svo/beta.npy')
[19]:
niw = 300
wn = np.pi / beta * (2. * np.arange(niw) + 1.)
# here we want a non-equispaced grid to cover a larger interval
w = 30 * np.tan(np.linspace(-np.pi/2.1, np.pi/2.1, num=501, endpoint=True)) / np.tan(np.pi / 2.1)
model = np.exp(-(w / 20)**6) # smooth cut-off at |w| > 20
model /= np.trapz(model, w) / 4.77 # normalization, not strictly necessary
probl = cont.AnalyticContinuationProblem(im_axis=wn,
re_axis=w,
im_data=siw[:niw]-hartree,
kernel_mode='freq_fermionic')
[20]:
sol, _ = probl.solve(method='maxent_svd',
optimizer='newton',
alpha_determination='chi2kink',
model=model,
stdev=err[:niw],
preblur=True,
blur_width=0.3,
interactive=True,
alpha_start=1e12,
alpha_end=1e-1)
501 data points on real axis
600 data points on imaginary axis
51 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 12.00, chi2 = 5.181e+07, S = -3.514e-10, nfev = 3, norm = 4.770
log10(alpha) = 11.00, chi2 = 5.179e+07, S = -3.513e-08, nfev = 9, norm = 4.770
log10(alpha) = 10.00, chi2 = 5.167e+07, S = -3.507e-06, nfev = 12, norm = 4.772
log10(alpha) = 9.00, chi2 = 5.042e+07, S = -3.444e-04, nfev = 16, norm = 4.787
log10(alpha) = 8.00, chi2 = 3.975e+07, S = -2.854e-02, nfev = 21, norm = 4.937
log10(alpha) = 7.00, chi2 = 9.856e+06, S = -5.861e-01, nfev = 53, norm = 5.640
log10(alpha) = 6.00, chi2 = 1.282e+06, S = -1.744e+00, nfev = 28, norm = 5.621
log10(alpha) = 5.00, chi2 = 9.610e+04, S = -3.252e+00, nfev = 31, norm = 5.080
log10(alpha) = 4.00, chi2 = 6.853e+03, S = -4.306e+00, nfev = 27, norm = 4.853
log10(alpha) = 3.00, chi2 = 5.785e+02, S = -5.065e+00, nfev = 45, norm = 4.782
log10(alpha) = 2.00, chi2 = 2.517e+02, S = -5.413e+00, nfev = 60, norm = 4.767
log10(alpha) = 1.00, chi2 = 2.330e+02, S = -5.760e+00, nfev = 64, norm = 4.766
log10(alpha) = 0.00, chi2 = 2.174e+02, S = -8.239e+00, nfev = 50, norm = 4.769
log10(alpha) = -1.00, chi2 = 2.132e+02, S = -1.370e+01, nfev = 56, norm = 4.770
Fit parameters [2.25041422 5.51210904 5.05097152 0.98324766]
Optimal log alpha 2.50837711444609
log10(alpha) = 2.51, chi2 = 3.032e+02, S = -5.284e+00, nfev = 36, norm = 4.771
[21]:
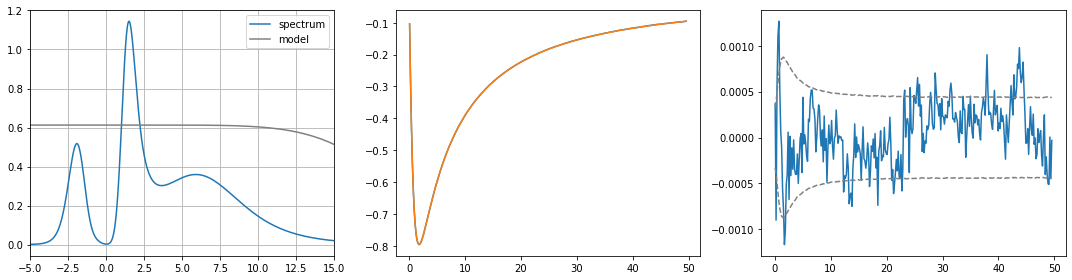
fig, ax = plt.subplots(ncols=3, nrows=1, figsize=(15, 4))
ax[0].plot(w, sol.A_opt, label='spectrum')
ax[0].plot(w, model * sol.norm, color='gray', label='model')
ax[0].legend()
ax[0].set_xlim(-5., 15.)
ax[0].grid()
ax[1].plot(wn, siw.imag[:niw])
ax[1].plot(wn, sol.backtransform.imag)
ax[2].plot(wn, (siw[:niw] - sol.backtransform).imag)
ax[2].plot(wn, err[:niw], ls='--', color='gray')
ax[2].plot(wn, -err[:niw], ls='--', color='gray')
plt.tight_layout()
plt.show()
6. Analytical continuation of a matrix-valued function (Kagome)¶
As an example for matrix-valued analytical continuation we take a D\(\Gamma\)A self-energy for the kagome Hubbard model at \(U=6t\), \(\beta=3/t\), half-filling, for a certain \(\mathbf{k}\)-point.
There, the self-energy is a 3$:nbsphinx-math:times`$3-matrix, with non-zero offdiagonal elements. In this case we are lucky and the projection of the self-energy on the eigenstates of the tight-binding Hamiltonian for this :math:mathbf{k}`-point is diagonal. This means that here we have two ways of doing the analytic continuation: 1. Via projections: * Project self-energy on eigenbasis of tb-Hamiltonian * Continue only the diagonal elements (standard problem) * Rotate back to original basis 2. Direct * Continue the diagonal elements in original basis (standard problem) * construct better default model for offdiag elements * continue the offdiag elements (pos-neg problem)
In the end we can compare both results.
[22]:
# load data
siw = np.load('data/kagome_offdiag/siw.npy') # DGA self-energy at certain k-point
states = np.load('data/kagome_offdiag/states.npy') # eigenstates of tb-Hamiltonian at this k-point
hartree = 3. # for U=6 and half-filling
beta = 3.
niw = siw.shape[0]
wn = np.pi / beta * (2. * np.arange(niw) + 1.)
[23]:
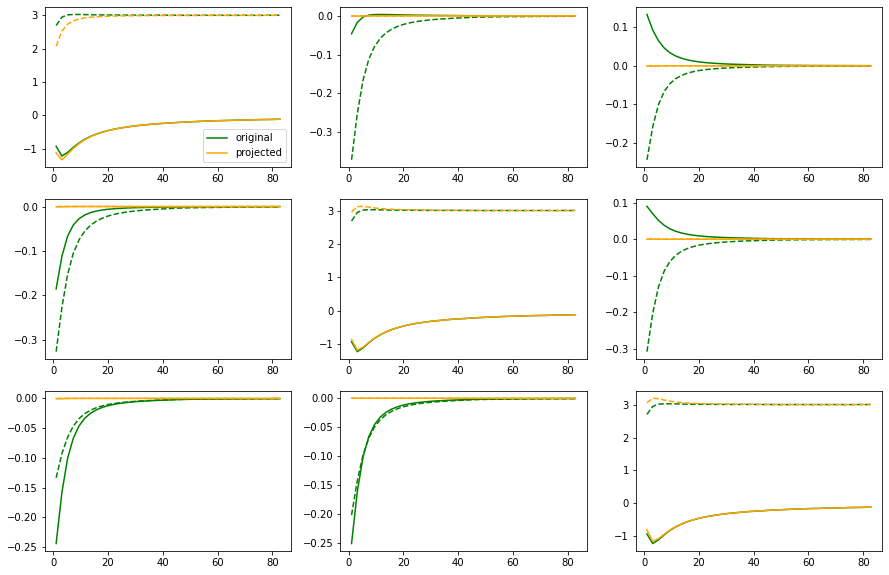
# project self-energy to Hamiltonian eigenbasis
siw_projected = states.T.conj() @ siw @ states
# plot original and projected matrix elements
fig, ax = plt.subplots(ncols=3, nrows=3, figsize=(15, 10))
for i in [0, 1, 2]:
for j in [0, 1, 2]:
ax[i, j].plot(wn, siw[:, i, j].real, color='green', ls='--')
ax[i, j].plot(wn, siw[:, i, j].imag, color='green', ls='-', label='original')
ax[i, j].plot(wn, siw_projected[:, i, j].real, color='orange', ls='--')
ax[i, j].plot(wn, siw_projected[:, i, j].imag, color='orange', ls='-', label='projected')
ax[0, 0].legend()
plt.show()
[24]:
# define real frequencies, default model and error for continuation
nw = 401
w = np.linspace(-20., 20., num=nw, endpoint=True)
model = np.ones_like(w)
model /= np.trapz(model, w) / 9. # for U=6 and half-filling, the norm is 9.
wn = np.pi / beta * (2. * np.arange(niw) + 1.)
err = np.ones_like(wn) * 2e-3
sw_diag = np.zeros((nw, 3, 3), dtype=complex)
for i in [0, 1, 2]: # we have 3 eigenmodes
# specify the problem
probl = cont.AnalyticContinuationProblem(im_axis=wn,
re_axis=w,
im_data=siw_projected[:, i, i] - hartree, # subtract Hartree term
kernel_mode='freq_fermionic')
# solve the problem
sol, _ = probl.solve(method='maxent_svd',
optimizer='newton',
alpha_determination='chi2kink',
model=model,
stdev=err,
interactive=True)
# get full self-energy from Kramers Kronig
sw_diag[:, i, i] = cont.GreensFunction(spectrum=sol.A_opt, wgrid=w, kind='fermionic').kkt() + hartree
# plot
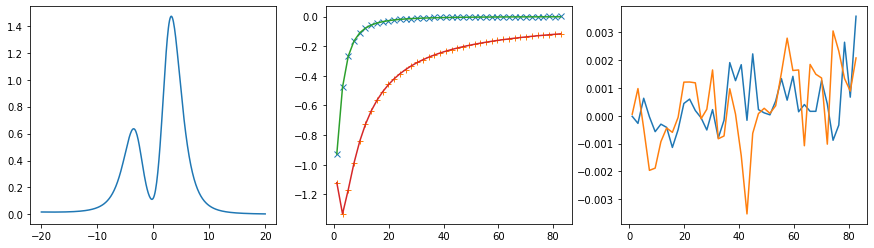
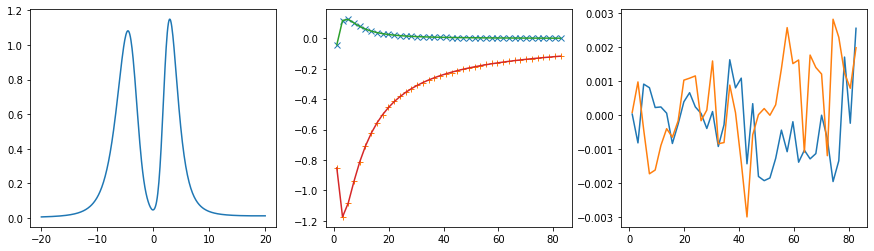
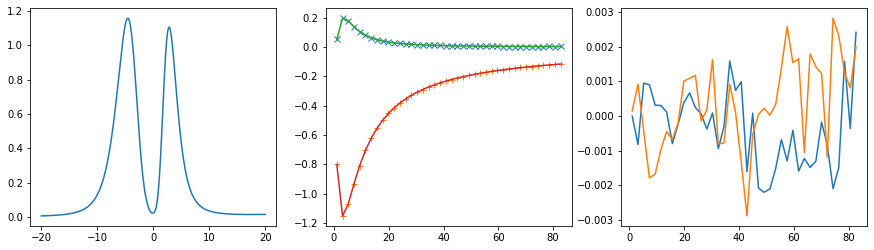
fig, ax = plt.subplots(ncols=3, nrows=1, figsize=(15, 4))
ax[0].plot(w, sol.A_opt)
ax[1].plot(wn, siw_projected[:, i, i].real - hartree, marker='x', ls='None')
ax[1].plot(wn, siw_projected[:, i, i].imag, marker='+', ls='None')
ax[1].plot(wn, sol.backtransform.real)
ax[1].plot(wn, sol.backtransform.imag)
ax[2].plot(wn, (siw_projected[:, i, i] - hartree - sol.backtransform).real)
ax[2].plot(wn, (siw_projected[:, i, i] - hartree - sol.backtransform).imag)
plt.show()
# go back to original basis
sw_rotated_back = states @ sw_diag @ states.T.conj()
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00, chi2 = 6.783e+05, S = -4.278e-08, nfev = 4, norm = 9.001
log10(alpha) = 8.00, chi2 = 6.767e+05, S = -4.272e-06, nfev = 11, norm = 9.005
log10(alpha) = 7.00, chi2 = 6.615e+05, S = -4.214e-04, nfev = 14, norm = 9.050
log10(alpha) = 6.00, chi2 = 5.274e+05, S = -3.608e-02, nfev = 17, norm = 9.466
log10(alpha) = 5.00, chi2 = 1.281e+05, S = -7.818e-01, nfev = 19, norm = 11.124
log10(alpha) = 4.00, chi2 = 2.349e+04, S = -2.224e+00, nfev = 20, norm = 11.403
log10(alpha) = 3.00, chi2 = 1.953e+03, S = -5.132e+00, nfev = 39, norm = 10.332
log10(alpha) = 2.00, chi2 = 1.346e+02, S = -7.279e+00, nfev = 37, norm = 9.823
log10(alpha) = 1.00, chi2 = 2.966e+01, S = -8.397e+00, nfev = 35, norm = 9.684
log10(alpha) = 0.00, chi2 = 2.604e+01, S = -8.865e+00, nfev = 46, norm = 9.663
log10(alpha) = -1.00, chi2 = 2.551e+01, S = -9.576e+00, nfev = 26, norm = 9.665
log10(alpha) = -2.00, chi2 = 2.540e+01, S = -1.143e+01, nfev = 28, norm = 9.666
log10(alpha) = -3.00, chi2 = 2.535e+01, S = -1.939e+01, nfev = 31, norm = 9.667
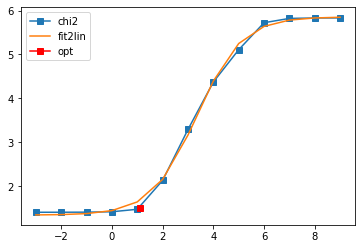
Fit parameters [1.34029571 4.51440873 3.34634067 1.12696789]
Optimal log alpha 1.1279988482793266
log10(alpha) = 1.13, chi2 = 3.146e+01, S = -8.320e+00, nfev = 14, norm = 9.691
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00, chi2 = 2.587e+05, S = -1.459e-08, nfev = 4, norm = 9.000
log10(alpha) = 8.00, chi2 = 2.581e+05, S = -1.455e-06, nfev = 10, norm = 9.004
log10(alpha) = 7.00, chi2 = 2.530e+05, S = -1.423e-04, nfev = 14, norm = 9.040
log10(alpha) = 6.00, chi2 = 2.101e+05, S = -1.138e-02, nfev = 17, norm = 9.364
log10(alpha) = 5.00, chi2 = 8.735e+04, S = -2.497e-01, nfev = 18, norm = 10.733
log10(alpha) = 4.00, chi2 = 2.374e+04, S = -1.311e+00, nfev = 20, norm = 11.318
log10(alpha) = 3.00, chi2 = 2.221e+03, S = -4.292e+00, nfev = 35, norm = 10.354
log10(alpha) = 2.00, chi2 = 1.513e+02, S = -6.728e+00, nfev = 37, norm = 9.831
log10(alpha) = 1.00, chi2 = 2.791e+01, S = -8.065e+00, nfev = 45, norm = 9.683
log10(alpha) = 0.00, chi2 = 2.456e+01, S = -8.398e+00, nfev = 23, norm = 9.657
log10(alpha) = -1.00, chi2 = 2.444e+01, S = -8.599e+00, nfev = 52, norm = 9.655
log10(alpha) = -2.00, chi2 = 2.438e+01, S = -9.493e+00, nfev = 26, norm = 9.657
log10(alpha) = -3.00, chi2 = 2.436e+01, S = -1.312e+01, nfev = 29, norm = 9.657
Fit parameters [1.32887755 4.07280426 3.0878616 1.23959631]
Optimal log alpha 1.0710759853132283
log10(alpha) = 1.07, chi2 = 2.901e+01, S = -8.015e+00, nfev = 12, norm = 9.688

401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00, chi2 = 2.592e+05, S = -1.385e-08, nfev = 4, norm = 9.000
log10(alpha) = 8.00, chi2 = 2.587e+05, S = -1.382e-06, nfev = 10, norm = 9.004
log10(alpha) = 7.00, chi2 = 2.538e+05, S = -1.352e-04, nfev = 13, norm = 9.039
log10(alpha) = 6.00, chi2 = 2.129e+05, S = -1.087e-02, nfev = 17, norm = 9.350
log10(alpha) = 5.00, chi2 = 9.153e+04, S = -2.497e-01, nfev = 18, norm = 10.698
log10(alpha) = 4.00, chi2 = 2.489e+04, S = -1.360e+00, nfev = 20, norm = 11.318
log10(alpha) = 3.00, chi2 = 2.364e+03, S = -4.505e+00, nfev = 36, norm = 10.354
log10(alpha) = 2.00, chi2 = 1.469e+02, S = -7.057e+00, nfev = 36, norm = 9.829
log10(alpha) = 1.00, chi2 = 2.922e+01, S = -8.340e+00, nfev = 46, norm = 9.684
log10(alpha) = 0.00, chi2 = 2.578e+01, S = -8.695e+00, nfev = 36, norm = 9.658
log10(alpha) = -1.00, chi2 = 2.558e+01, S = -9.015e+00, nfev = 39, norm = 9.657
log10(alpha) = -2.00, chi2 = 2.549e+01, S = -1.046e+01, nfev = 27, norm = 9.659
log10(alpha) = -3.00, chi2 = 2.546e+01, S = -1.500e+01, nfev = 30, norm = 9.659
Fit parameters [1.35107894 4.04894961 3.08105855 1.26503099]
Optimal log alpha 1.1048223759601463
log10(alpha) = 1.10, chi2 = 3.094e+01, S = -8.265e+00, nfev = 13, norm = 9.690
[25]:
sw_full = np.zeros_like(sw_diag)
# first loop only over the diagonal elements
for i in [0, 1, 2]:
print('Diagonal element {}'.format(i))
# specify the problem
probl = cont.AnalyticContinuationProblem(im_axis=wn,
re_axis=w,
im_data=siw[:, i, i] - hartree, # subtract Hartree term
kernel_mode='freq_fermionic')
# solve the problem
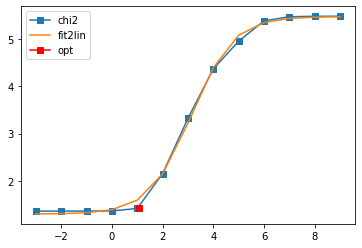
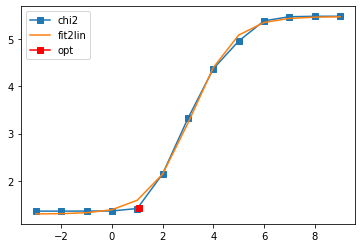
sol, _ = probl.solve(method='maxent_svd',
optimizer='newton',
alpha_determination='chi2kink',
model=model,
stdev=err,
interactive=True)
# construct full self-energy by Kramers Kronig
sw_full[:, i, i] = cont.GreensFunction(spectrum=sol.A_opt, wgrid=w, kind='fermionic').kkt() + hartree
# plot
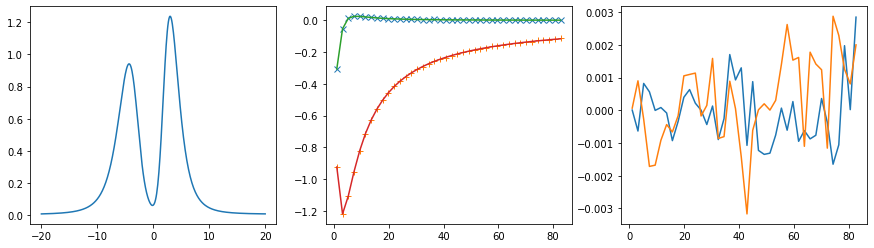
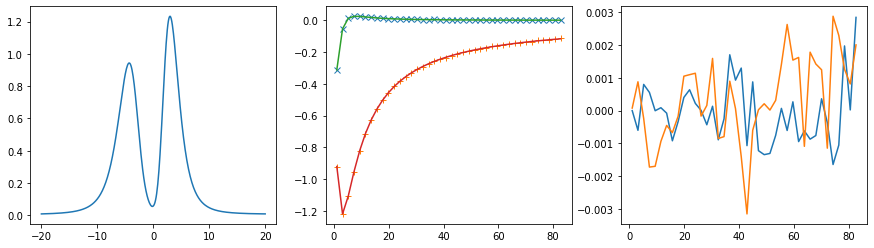
fig, ax = plt.subplots(ncols=3, nrows=1, figsize=(15, 4))
ax[0].plot(w, sol.A_opt)
ax[1].plot(wn, siw[:, i, i].real - hartree, marker='x', ls='None')
ax[1].plot(wn, siw[:, i, i].imag, marker='+', ls='None')
ax[1].plot(wn, sol.backtransform.real)
ax[1].plot(wn, sol.backtransform.imag)
ax[2].plot(wn, (siw[:, i, i] - hartree - sol.backtransform).real)
ax[2].plot(wn, (siw[:, i, i] - hartree - sol.backtransform).imag)
plt.show()
# now loop over the offdiagonal elements
for i in [0, 1, 2]:
for j in [0, 1, 2]:
if i == j: continue
print('Offdiagonal element {} {}'.format(i, j))
# construct a good default model
offdiag_model = np.sqrt(sw_full.imag[:, i, i] * sw_full.imag[:, j, j]) # "poorman's method" Kraberger et al.
# specify the problem
probl = cont.AnalyticContinuationProblem(im_axis=wn,
re_axis=w,
im_data=siw[:, i, j], # no Hartree term here!
kernel_mode='freq_fermionic')
# solve the problem
sol, _ = probl.solve(method='maxent_svd',
optimizer='newton',
alpha_determination='chi2kink',
model=offdiag_model, # switch on offdiag mode
stdev=err,
offdiag=True,
alpha_start=1e10,
alpha_end=1e-6,
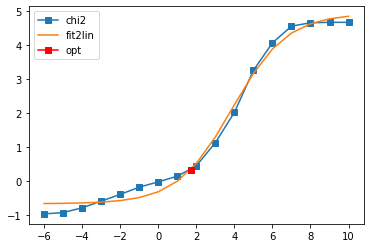
fit_position=1.5, # smaller value to prevent overfitting
interactive=True)
# construct full self-energy by Kramers Kronig
sw_full[:, i, j] = cont.GreensFunction(spectrum=sol.A_opt, wgrid=w, kind='fermionic').kkt()
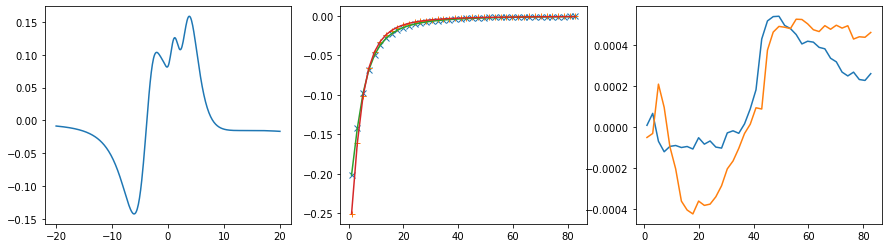
# plot
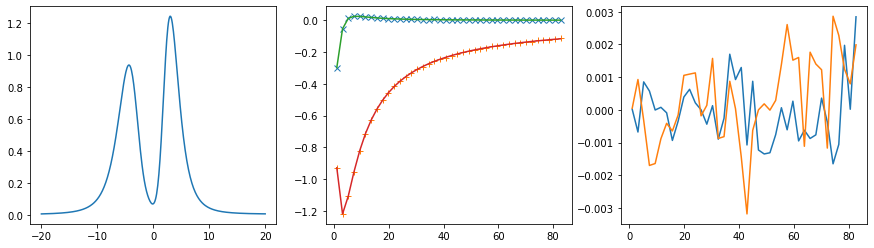
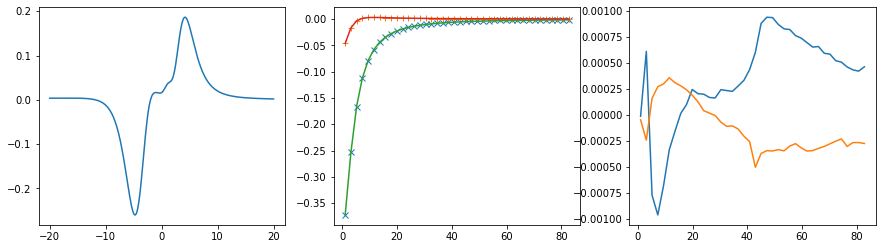
fig, ax = plt.subplots(ncols=3, nrows=1, figsize=(15, 4))
ax[0].plot(w, sol.A_opt)
ax[1].plot(wn, siw[:, i, j].real, marker='x', ls='None')
ax[1].plot(wn, siw[:, i, j].imag, marker='+', ls='None')
ax[1].plot(wn, sol.backtransform.real)
ax[1].plot(wn, sol.backtransform.imag)
ax[2].plot(wn, (siw[:, i, j] - sol.backtransform).real)
ax[2].plot(wn, (siw[:, i, j] - sol.backtransform).imag)
plt.show()
Diagonal element 0
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00, chi2 = 3.003e+05, S = -1.797e-08, nfev = 4, norm = 9.000
log10(alpha) = 8.00, chi2 = 2.996e+05, S = -1.793e-06, nfev = 10, norm = 9.004
log10(alpha) = 7.00, chi2 = 2.933e+05, S = -1.755e-04, nfev = 14, norm = 9.043
log10(alpha) = 6.00, chi2 = 2.400e+05, S = -1.417e-02, nfev = 17, norm = 9.389
log10(alpha) = 5.00, chi2 = 8.949e+04, S = -3.016e-01, nfev = 18, norm = 10.814
log10(alpha) = 4.00, chi2 = 2.324e+04, S = -1.381e+00, nfev = 20, norm = 11.331
log10(alpha) = 3.00, chi2 = 2.095e+03, S = -4.284e+00, nfev = 44, norm = 10.348
log10(alpha) = 2.00, chi2 = 1.421e+02, S = -6.596e+00, nfev = 38, norm = 9.830
log10(alpha) = 1.00, chi2 = 2.607e+01, S = -7.838e+00, nfev = 31, norm = 9.684
log10(alpha) = 0.00, chi2 = 2.308e+01, S = -8.137e+00, nfev = 28, norm = 9.657
log10(alpha) = -1.00, chi2 = 2.298e+01, S = -8.278e+00, nfev = 48, norm = 9.653
log10(alpha) = -2.00, chi2 = 2.293e+01, S = -9.278e+00, nfev = 48, norm = 9.653
log10(alpha) = -3.00, chi2 = 2.290e+01, S = -1.440e+01, nfev = 29, norm = 9.652
Fit parameters [1.29842143 4.17127903 3.12916432 1.21176069]
Optimal log alpha 1.0660506905566396
log10(alpha) = 1.07, chi2 = 2.697e+01, S = -7.796e+00, nfev = 12, norm = 9.688
Diagonal element 1
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00, chi2 = 3.010e+05, S = -1.795e-08, nfev = 4, norm = 9.000
log10(alpha) = 8.00, chi2 = 3.004e+05, S = -1.791e-06, nfev = 10, norm = 9.004
log10(alpha) = 7.00, chi2 = 2.940e+05, S = -1.753e-04, nfev = 14, norm = 9.043
log10(alpha) = 6.00, chi2 = 2.408e+05, S = -1.416e-02, nfev = 17, norm = 9.389
log10(alpha) = 5.00, chi2 = 9.008e+04, S = -3.022e-01, nfev = 18, norm = 10.814
log10(alpha) = 4.00, chi2 = 2.340e+04, S = -1.389e+00, nfev = 20, norm = 11.332
log10(alpha) = 3.00, chi2 = 2.099e+03, S = -4.314e+00, nfev = 44, norm = 10.347
log10(alpha) = 2.00, chi2 = 1.402e+02, S = -6.623e+00, nfev = 38, norm = 9.830
log10(alpha) = 1.00, chi2 = 2.604e+01, S = -7.844e+00, nfev = 31, norm = 9.684
log10(alpha) = 0.00, chi2 = 2.308e+01, S = -8.141e+00, nfev = 28, norm = 9.657
log10(alpha) = -1.00, chi2 = 2.298e+01, S = -8.284e+00, nfev = 47, norm = 9.653
log10(alpha) = -2.00, chi2 = 2.293e+01, S = -9.296e+00, nfev = 46, norm = 9.653
log10(alpha) = -3.00, chi2 = 2.290e+01, S = -1.446e+01, nfev = 29, norm = 9.652
Fit parameters [1.29883645 4.17134996 3.12935829 1.2159353 ]
Optimal log alpha 1.0733278533586619
log10(alpha) = 1.07, chi2 = 2.704e+01, S = -7.798e+00, nfev = 12, norm = 9.689
Diagonal element 2
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 9.00, chi2 = 2.994e+05, S = -1.801e-08, nfev = 4, norm = 9.000
log10(alpha) = 8.00, chi2 = 2.987e+05, S = -1.797e-06, nfev = 10, norm = 9.004
log10(alpha) = 7.00, chi2 = 2.924e+05, S = -1.759e-04, nfev = 14, norm = 9.043
log10(alpha) = 6.00, chi2 = 2.390e+05, S = -1.420e-02, nfev = 17, norm = 9.390
log10(alpha) = 5.00, chi2 = 8.866e+04, S = -3.010e-01, nfev = 18, norm = 10.815
log10(alpha) = 4.00, chi2 = 2.303e+04, S = -1.370e+00, nfev = 20, norm = 11.330
log10(alpha) = 3.00, chi2 = 2.089e+03, S = -4.243e+00, nfev = 45, norm = 10.349
log10(alpha) = 2.00, chi2 = 1.450e+02, S = -6.559e+00, nfev = 38, norm = 9.831
log10(alpha) = 1.00, chi2 = 2.612e+01, S = -7.832e+00, nfev = 35, norm = 9.684
log10(alpha) = 0.00, chi2 = 2.307e+01, S = -8.135e+00, nfev = 35, norm = 9.657
log10(alpha) = -1.00, chi2 = 2.298e+01, S = -8.274e+00, nfev = 55, norm = 9.653
log10(alpha) = -2.00, chi2 = 2.293e+01, S = -9.260e+00, nfev = 49, norm = 9.653
log10(alpha) = -3.00, chi2 = 2.290e+01, S = -1.433e+01, nfev = 29, norm = 9.652
Fit parameters [1.29780736 4.17145334 3.12884244 1.205656 ]
Optimal log alpha 1.0552824850877567
log10(alpha) = 1.06, chi2 = 2.687e+01, S = -7.797e+00, nfev = 12, norm = 9.687
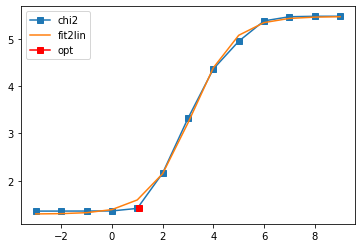
Offdiagonal element 0 1
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 10.00, chi2 = 6.525e+04, S = -4.689e-10, nfev = 1, norm = 0.000
log10(alpha) = 9.00, chi2 = 6.508e+04, S = -4.676e-08, nfev = 3, norm = 0.000
log10(alpha) = 8.00, chi2 = 6.344e+04, S = -4.552e-06, nfev = 9, norm = 0.003
log10(alpha) = 7.00, chi2 = 5.003e+04, S = -3.542e-04, nfev = 13, norm = 0.018
log10(alpha) = 6.00, chi2 = 1.220e+04, S = -7.678e-03, nfev = 19, norm = 0.009
log10(alpha) = 5.00, chi2 = 9.045e+02, S = -2.131e-02, nfev = 21, norm = -0.079
log10(alpha) = 4.00, chi2 = 5.157e+01, S = -3.166e-02, nfev = 16, norm = -0.080
log10(alpha) = 3.00, chi2 = 7.075e+00, S = -3.665e-02, nfev = 25, norm = -0.048
log10(alpha) = 2.00, chi2 = 2.438e+00, S = -4.344e-02, nfev = 16, norm = -0.029
log10(alpha) = 1.00, chi2 = 1.600e+00, S = -5.622e-02, nfev = 26, norm = -0.020
log10(alpha) = 0.00, chi2 = 1.265e+00, S = -1.187e-01, nfev = 18, norm = -0.015
log10(alpha) = -1.00, chi2 = 9.880e-01, S = -6.166e-01, nfev = 20, norm = -0.010
log10(alpha) = -2.00, chi2 = 6.846e-01, S = -6.943e+00, nfev = 72, norm = -0.007
log10(alpha) = -3.00, chi2 = 4.620e-01, S = -5.035e+01, nfev = 74, norm = -0.005
log10(alpha) = -4.00, chi2 = 2.742e-01, S = -3.289e+02, nfev = 88, norm = -0.005
log10(alpha) = -5.00, chi2 = 1.697e-01, S = -2.243e+03, nfev = 127, norm = -0.007
log10(alpha) = -6.00, chi2 = 1.462e-01, S = -6.135e+03, nfev = 62, norm = -0.011
Fit parameters [-0.39097276 5.43464373 4.36226097 0.80648082]
Optimal log alpha 2.502328332228192
log10(alpha) = 2.50, chi2 = 3.918e+00, S = -3.943e-02, nfev = 12, norm = -0.036
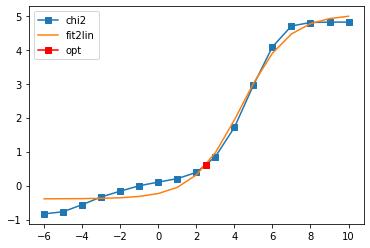
Offdiagonal element 0 2
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 10.00, chi2 = 3.497e+04, S = -2.028e-10, nfev = 1, norm = -0.000
log10(alpha) = 9.00, chi2 = 3.490e+04, S = -2.023e-08, nfev = 2, norm = -0.001
log10(alpha) = 8.00, chi2 = 3.418e+04, S = -1.978e-06, nfev = 9, norm = -0.006
log10(alpha) = 7.00, chi2 = 2.817e+04, S = -1.601e-04, nfev = 12, norm = -0.053
log10(alpha) = 6.00, chi2 = 8.684e+03, S = -4.093e-03, nfev = 16, norm = -0.266
log10(alpha) = 5.00, chi2 = 8.224e+02, S = -1.443e-02, nfev = 16, norm = -0.337
log10(alpha) = 4.00, chi2 = 8.786e+01, S = -2.348e-02, nfev = 17, norm = -0.215
log10(alpha) = 3.00, chi2 = 1.631e+01, S = -3.355e-02, nfev = 20, norm = -0.126
log10(alpha) = 2.00, chi2 = 2.891e+00, S = -5.109e-02, nfev = 23, norm = -0.076
log10(alpha) = 1.00, chi2 = 1.253e+00, S = -7.461e-02, nfev = 26, norm = -0.053
log10(alpha) = 0.00, chi2 = 7.296e-01, S = -1.677e-01, nfev = 18, norm = -0.040
log10(alpha) = -1.00, chi2 = 4.765e-01, S = -6.223e-01, nfev = 19, norm = -0.029
log10(alpha) = -2.00, chi2 = 2.909e-01, S = -3.844e+00, nfev = 72, norm = -0.020
log10(alpha) = -3.00, chi2 = 1.945e-01, S = -2.190e+01, nfev = 85, norm = -0.012
log10(alpha) = -4.00, chi2 = 1.311e-01, S = -1.214e+02, nfev = 40, norm = -0.007
log10(alpha) = -5.00, chi2 = 9.567e-02, S = -8.655e+02, nfev = 88, norm = -0.006
log10(alpha) = -6.00, chi2 = 7.966e-02, S = -3.558e+03, nfev = 41, norm = -0.011
Fit parameters [-0.84341047 5.72437401 3.83747472 0.61814642]
Optimal log alpha 1.410865161600237
log10(alpha) = 1.41, chi2 = 1.628e+00, S = -6.305e-02, nfev = 12, norm = -0.060
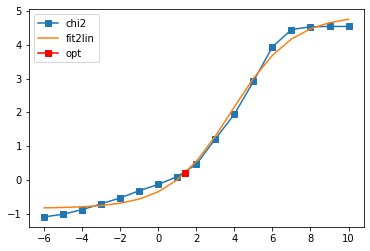
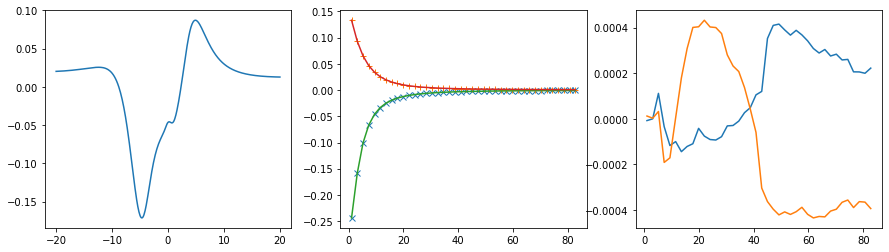
Offdiagonal element 1 0
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 10.00, chi2 = 6.523e+04, S = -4.929e-10, nfev = 1, norm = 0.000
log10(alpha) = 9.00, chi2 = 6.505e+04, S = -4.915e-08, nfev = 3, norm = 0.001
log10(alpha) = 8.00, chi2 = 6.332e+04, S = -4.772e-06, nfev = 9, norm = 0.009
log10(alpha) = 7.00, chi2 = 4.951e+04, S = -3.635e-04, nfev = 13, norm = 0.076
log10(alpha) = 6.00, chi2 = 1.316e+04, S = -7.272e-03, nfev = 15, norm = 0.263
log10(alpha) = 5.00, chi2 = 1.551e+03, S = -2.290e-02, nfev = 15, norm = 0.203
log10(alpha) = 4.00, chi2 = 6.559e+01, S = -4.067e-02, nfev = 16, norm = 0.087
log10(alpha) = 3.00, chi2 = 6.448e+00, S = -4.680e-02, nfev = 17, norm = 0.048
log10(alpha) = 2.00, chi2 = 2.318e+00, S = -5.281e-02, nfev = 16, norm = 0.029
log10(alpha) = 1.00, chi2 = 1.561e+00, S = -6.424e-02, nfev = 26, norm = 0.021
log10(alpha) = 0.00, chi2 = 1.270e+00, S = -1.196e-01, nfev = 24, norm = 0.016
log10(alpha) = -1.00, chi2 = 9.898e-01, S = -6.360e-01, nfev = 38, norm = 0.012
log10(alpha) = -2.00, chi2 = 6.704e-01, S = -7.233e+00, nfev = 102, norm = 0.007
log10(alpha) = -3.00, chi2 = 4.413e-01, S = -5.117e+01, nfev = 61, norm = 0.001
log10(alpha) = -4.00, chi2 = 2.615e-01, S = -3.186e+02, nfev = 83, norm = -0.002
log10(alpha) = -5.00, chi2 = 1.667e-01, S = -2.055e+03, nfev = 122, norm = -0.005
log10(alpha) = -6.00, chi2 = 1.488e-01, S = -4.818e+03, nfev = 52, norm = -0.006
Fit parameters [-0.39264746 5.3892644 4.25688119 0.84949537]
Optimal log alpha 2.4911270061596706
log10(alpha) = 2.49, chi2 = 3.578e+00, S = -4.934e-02, nfev = 12, norm = 0.037
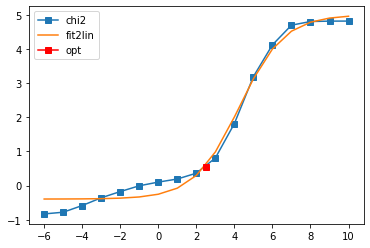
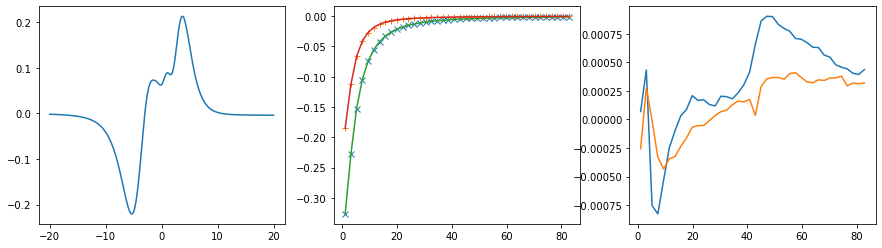
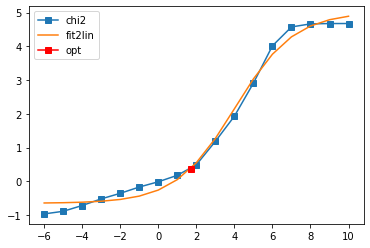
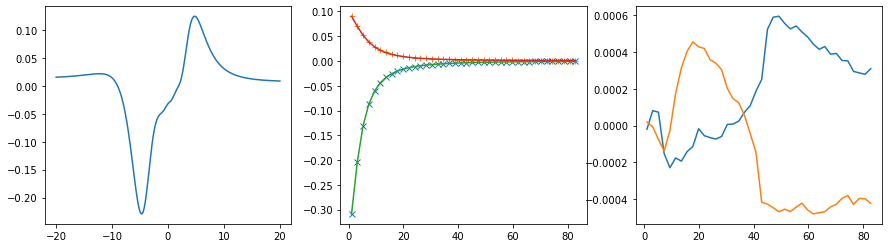
Offdiagonal element 1 2
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 10.00, chi2 = 4.747e+04, S = -2.987e-10, nfev = 1, norm = -0.000
log10(alpha) = 9.00, chi2 = 4.736e+04, S = -2.980e-08, nfev = 3, norm = -0.000
log10(alpha) = 8.00, chi2 = 4.631e+04, S = -2.910e-06, nfev = 9, norm = -0.004
log10(alpha) = 7.00, chi2 = 3.755e+04, S = -2.328e-04, nfev = 13, norm = -0.037
log10(alpha) = 6.00, chi2 = 1.036e+04, S = -5.645e-03, nfev = 16, norm = -0.211
log10(alpha) = 5.00, chi2 = 8.102e+02, S = -1.752e-02, nfev = 15, norm = -0.296
log10(alpha) = 4.00, chi2 = 8.474e+01, S = -2.655e-02, nfev = 17, norm = -0.199
log10(alpha) = 3.00, chi2 = 1.522e+01, S = -3.605e-02, nfev = 27, norm = -0.116
log10(alpha) = 2.00, chi2 = 3.075e+00, S = -5.217e-02, nfev = 17, norm = -0.070
log10(alpha) = 1.00, chi2 = 1.498e+00, S = -7.510e-02, nfev = 26, norm = -0.049
log10(alpha) = 0.00, chi2 = 9.631e-01, S = -1.713e-01, nfev = 18, norm = -0.036
log10(alpha) = -1.00, chi2 = 6.728e-01, S = -6.903e-01, nfev = 27, norm = -0.027
log10(alpha) = -2.00, chi2 = 4.379e-01, S = -5.034e+00, nfev = 71, norm = -0.017
log10(alpha) = -3.00, chi2 = 2.997e-01, S = -3.111e+01, nfev = 85, norm = -0.010
log10(alpha) = -4.00, chi2 = 1.906e-01, S = -1.983e+02, nfev = 36, norm = -0.007
log10(alpha) = -5.00, chi2 = 1.283e-01, S = -1.436e+03, nfev = 108, norm = -0.007
log10(alpha) = -6.00, chi2 = 1.073e-01, S = -4.961e+03, nfev = 64, norm = -0.012
Fit parameters [-0.65366492 5.66409807 4.03328656 0.64482825]
Optimal log alpha 1.7070857589775366
log10(alpha) = 1.71, chi2 = 2.324e+00, S = -5.737e-02, nfev = 20, norm = -0.062
Offdiagonal element 2 0
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 10.00, chi2 = 3.499e+04, S = -2.410e-10, nfev = 1, norm = 0.000
log10(alpha) = 9.00, chi2 = 3.490e+04, S = -2.402e-08, nfev = 2, norm = 0.001
log10(alpha) = 8.00, chi2 = 3.406e+04, S = -2.331e-06, nfev = 9, norm = 0.012
log10(alpha) = 7.00, chi2 = 2.734e+04, S = -1.765e-04, nfev = 12, norm = 0.101
log10(alpha) = 6.00, chi2 = 9.609e+03, S = -3.584e-03, nfev = 15, norm = 0.402
log10(alpha) = 5.00, chi2 = 1.559e+03, S = -1.607e-02, nfev = 16, norm = 0.399
log10(alpha) = 4.00, chi2 = 1.045e+02, S = -3.359e-02, nfev = 19, norm = 0.220
log10(alpha) = 3.00, chi2 = 1.491e+01, S = -4.495e-02, nfev = 19, norm = 0.126
log10(alpha) = 2.00, chi2 = 2.747e+00, S = -6.085e-02, nfev = 24, norm = 0.076
log10(alpha) = 1.00, chi2 = 1.197e+00, S = -8.279e-02, nfev = 33, norm = 0.053
log10(alpha) = 0.00, chi2 = 7.387e-01, S = -1.655e-01, nfev = 25, norm = 0.040
log10(alpha) = -1.00, chi2 = 4.813e-01, S = -6.434e-01, nfev = 49, norm = 0.030
log10(alpha) = -2.00, chi2 = 2.774e-01, S = -4.180e+00, nfev = 34, norm = 0.020
log10(alpha) = -3.00, chi2 = 1.689e-01, S = -2.425e+01, nfev = 70, norm = 0.011
log10(alpha) = -4.00, chi2 = 1.132e-01, S = -1.098e+02, nfev = 73, norm = 0.004
log10(alpha) = -5.00, chi2 = 8.941e-02, S = -5.790e+02, nfev = 62, norm = 0.000
log10(alpha) = -6.00, chi2 = 8.205e-02, S = -1.574e+03, nfev = 35, norm = 0.002
Fit parameters [-0.85180161 5.67618507 3.72214498 0.65382993]
Optimal log alpha 1.4279704254349954
log10(alpha) = 1.43, chi2 = 1.560e+00, S = -7.192e-02, nfev = 12, norm = 0.061
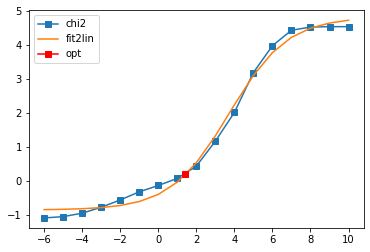
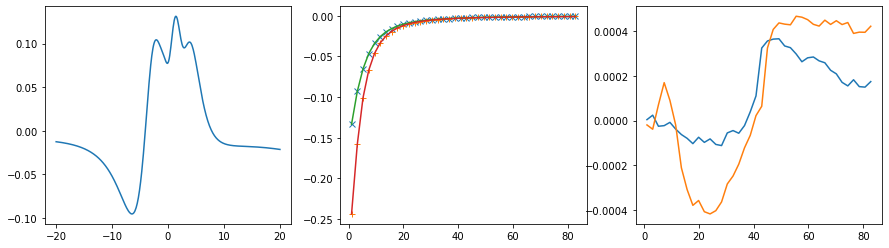
Offdiagonal element 2 1
401 data points on real axis
80 data points on imaginary axis
26 significant singular values
Precomputation of coefficient matrices...
log10(alpha) = 10.00, chi2 = 4.751e+04, S = -3.436e-10, nfev = 1, norm = 0.000
log10(alpha) = 9.00, chi2 = 4.738e+04, S = -3.426e-08, nfev = 2, norm = 0.001
log10(alpha) = 8.00, chi2 = 4.618e+04, S = -3.323e-06, nfev = 9, norm = 0.012
log10(alpha) = 7.00, chi2 = 3.663e+04, S = -2.511e-04, nfev = 12, norm = 0.104
log10(alpha) = 6.00, chi2 = 1.183e+04, S = -4.974e-03, nfev = 15, norm = 0.403
log10(alpha) = 5.00, chi2 = 1.842e+03, S = -2.002e-02, nfev = 18, norm = 0.385
log10(alpha) = 4.00, chi2 = 1.071e+02, S = -4.088e-02, nfev = 19, norm = 0.204
log10(alpha) = 3.00, chi2 = 1.381e+01, S = -5.215e-02, nfev = 19, norm = 0.116
log10(alpha) = 2.00, chi2 = 2.879e+00, S = -6.659e-02, nfev = 17, norm = 0.070
log10(alpha) = 1.00, chi2 = 1.428e+00, S = -8.733e-02, nfev = 40, norm = 0.049
log10(alpha) = 0.00, chi2 = 9.735e-01, S = -1.707e-01, nfev = 25, norm = 0.037
log10(alpha) = -1.00, chi2 = 6.780e-01, S = -7.193e-01, nfev = 39, norm = 0.028
log10(alpha) = -2.00, chi2 = 4.174e-01, S = -5.514e+00, nfev = 70, norm = 0.017
log10(alpha) = -3.00, chi2 = 2.640e-01, S = -3.380e+01, nfev = 48, norm = 0.008
log10(alpha) = -4.00, chi2 = 1.680e-01, S = -1.817e+02, nfev = 101, norm = 0.002
log10(alpha) = -5.00, chi2 = 1.218e-01, S = -1.083e+03, nfev = 91, norm = -0.001
log10(alpha) = -6.00, chi2 = 1.110e-01, S = -2.586e+03, nfev = 55, norm = 0.000
Fit parameters [-0.65452172 5.58782077 3.88284786 0.69667046]
Optimal log alpha 1.7297495431654122
log10(alpha) = 1.73, chi2 = 2.224e+00, S = -7.102e-02, nfev = 25, norm = 0.063
[26]:
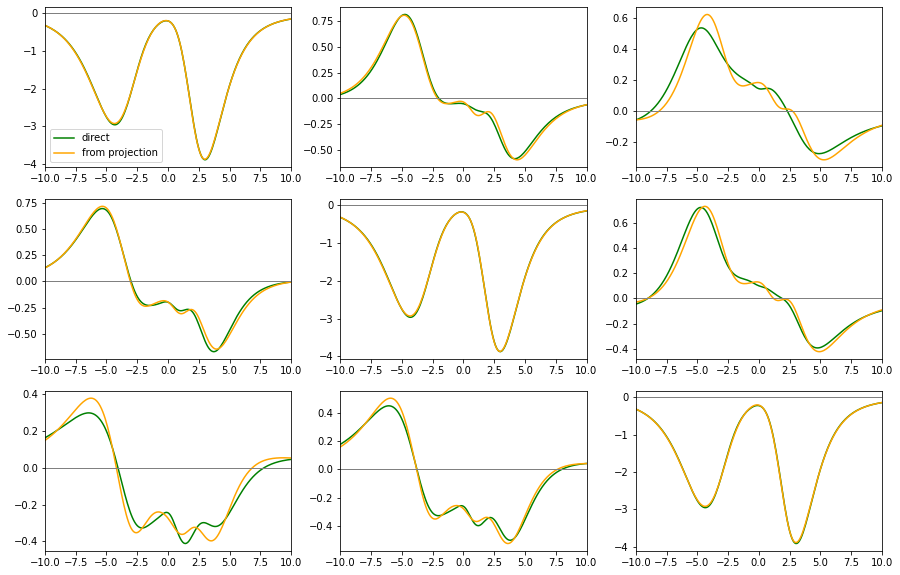
# now plot all matrix elements from both methods and compare
fig, ax = plt.subplots(ncols=3, nrows=3, figsize=(15, 10))
for i in [0, 1, 2]:
for j in [0, 1, 2]:
ax[i, j].plot(w, sw_full[:, i, j].imag, color='green', ls='-', label='direct')
ax[i, j].plot(w, sw_rotated_back[:, i, j].imag, color='orange', ls='-', label='from projection')
ax[i, j].set_xlim(-10., 10)
ax[i, j].axhline(0., color='gray', lw=1)
ax[0, 0].legend()
plt.show()
[ ]: